La mémoire de l’ordinateur fonctionne avec une série d’emplacements permettant d’accommoder les 0 et 1 que l’ordinateur utilise pour son fonctionnement. Chaque série de 0 et 1 correspond à un emplacement de mémoire nommé « bit » .

Les bits sont groupés en paquets de huits appelés « octets » pour représenter les chiffres, les lettres et les caractères spéciaux.

1	1	1	1	1	1	1	1
0	0	0	0	0	0	0	0

8 bits (français)

=

1 octet (français)

=

1 byte (anglais)

Le système décimal avec lequel nous travaillons régulièrement est constitué de 10 chiffres (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

Contrairement au système décimal, le système binaire n'utilise que les chiffres 0 et 1. Dans un ordinateur, le 0 représente l'état éteint et le 1 représente l'état allumé.

Tout ce qui entre dans un ordinateur est ainsi converti en système binaire par l'utilisation de ces deux chiffres.

Calculs mathématiques	Terme français		Terme français		Terme anglais
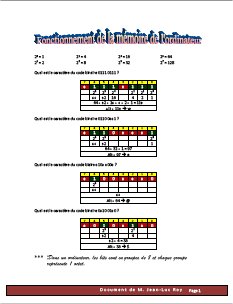
23	8 bits	=	1 octet	=	1 byte
2 4	16 bits	=	2 octets	=	2 bytes
2 5	32 bits	=	4 octets	=	4 bytes
2 6	64 bits	=	8 octets	=	8 bytes
2 7	128 bits	=	16 octets	=	16 bytes

Exemple de calculs qu'effectue l'ordinateur pour la manipulation de caractères

2⁰ = 1
2¹ = 2
2² = 4
2³ = 8
2⁴ = 16
2⁵ = 32
2⁶ = 64
2⁷ = 128

La représentation du caractère « a » pour un ordinateur est « 01100001 ».

Le tableau suivant démontre le calcul effectué par l'ordinateur lorsqu'il affiche à l'écran ou imprime le caractère « a ».



Le schéma ci-dessous les signaux électroniques des lettres F, I et N